FÍSICA GENERAL
ACTIVIDAD COLABORATIVA FASE II - (0 - 1)
Las Leyes de Movimiento y sus Aplicaciones.
1. En la máquina de Atwood que se muestra en la figura, 𝑚1 = 3.00 kg y 𝑚2 = 7.00 kg. La polea tiene masa despreciable y gira sin fricción. La cuerda es muy liviana e inextensible, y es larga a ambos costados. El objeto más ligero se libera con un empujón rápido que lo pone en movimiento a 2.40 m/s hacia abajo. ¿Qué distancia descenderá 𝑚1 por debajo del nivel donde fue liberado?.
2. La rapidez promedio de una molécula de nitrógeno en el aire es aproximadamente 6.70 × 10^2 m/s y su masa es 4.68 × 10^−26 kg. Si una molécula de nitrógeno tarda 3.00 × 10−13 s en contacto con una pared mientras la golpea, y rebota con la misma rapidez pero moviéndose en la dirección opuesta,
(a) ¿Cuál es la aceleración media de la molécula durante este intervalo de tiempo?
(b) ¿Qué fuerza media ejerce la molécula sobre la pared?
1. En la máquina de Atwood que se muestra en la figura, 𝑚1 = 3.00 kg y 𝑚2 = 7.00 kg. La polea tiene masa despreciable y gira sin fricción. La cuerda es muy liviana e inextensible, y es larga a ambos costados. El objeto más ligero se libera con un empujón rápido que lo pone en movimiento a 2.40 m/s hacia abajo. ¿Qué distancia descenderá 𝑚1 por debajo del nivel donde fue liberado?.
2. La rapidez promedio de una molécula de nitrógeno en el aire es aproximadamente 6.70 × 10^2 m/s y su masa es 4.68 × 10^−26 kg. Si una molécula de nitrógeno tarda 3.00 × 10−13 s en contacto con una pared mientras la golpea, y rebota con la misma rapidez pero moviéndose en la dirección opuesta,
(a) ¿Cuál es la aceleración media de la molécula durante este intervalo de tiempo?
(b) ¿Qué fuerza media ejerce la molécula sobre la pared?
Fuerzas de Fricción
3. Un disco de hockey sobre un lago se golpea y adquiere una velocidad inicial de 22.0 m/s. Si el disco siempre permanece sobre el hielo y se desliza 118 m antes de detenerse, determine el coeficiente de fricción cinética entre el disco y el hielo?
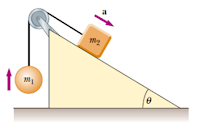
4. Dos masas desiguales están unidas por una cuerda ligera que pasa por una polea sin fricción. El bloque de m2, se ubica sobre un plano inclinado, con coeficiente de fricción 𝜇 y ángulo 𝜃.
(a) si m1=3.00 Kg, m2 = 10.0Kg y 𝜃=35.0⁰, calcule el valor del coeficiente de fricción para que el sistema tenga una aceleración de 0.828m/s2 y
(b) Calcule el valor de la tensión de la cuerda..
3. Un disco de hockey sobre un lago se golpea y adquiere una velocidad inicial de 22.0 m/s. Si el disco siempre permanece sobre el hielo y se desliza 118 m antes de detenerse, determine el coeficiente de fricción cinética entre el disco y el hielo?
4. Dos masas desiguales están unidas por una cuerda ligera que pasa por una polea sin fricción. El bloque de m2, se ubica sobre un plano inclinado, con coeficiente de fricción 𝜇 y ángulo 𝜃.
(a) si m1=3.00 Kg, m2 = 10.0Kg y 𝜃=35.0⁰, calcule el valor del coeficiente de fricción para que el sistema tenga una aceleración de 0.828m/s2 y
(b) Calcule el valor de la tensión de la cuerda..
Trabajo
5. Una fuerza 𝑭⃗ = (𝟑. 𝟎𝟎𝒊̂+ 𝟒. 𝟎𝟎𝒋̂)𝑵 actúa sobre una partícula. El ángulo entre 𝑭⃗ y el vector desplazamiento 𝒔⃗ es de 𝟑𝟐. 𝟎 𝒐 , y 𝑭⃗ efectúa 96. 0 J de trabajo. Determina el vector y la magnitud del vector 𝒔⃗ , teniendo en cuenta que el ángulo que forma el vector 𝒔⃗ con el x+ , es mayor que el ángulo que forma el vector 𝑭⃗ con el x+.
6. La fuerza que actúa sobre una partícula varía como se muestra en la figura. Encuentre el trabajo invertido por la fuerza en la partícula conforme se mueve…
(a) De 𝑥 = 0.00 𝑚 a 𝑥 = 8.00 m;
(b) de 𝑥 = 0.00 𝑚 a 𝑥 = 12.00 m.
(c) Existe cierto punto A sobre el eje X tal que el trabajo realizado por esta fuerza en el intervalo [𝑥𝐴 ,12.0 m] vale cero. Encuentre el valor de 𝑥𝐴 .
7. Una bala de 60 g se dispara de un rifle que tiene un cañón de 0.40m de largo. Se considera que el origen se sitúa donde la bala empieza a moverse. La fuerza en Newton, ejercida sobre la bala por la expansión del gas es 15 ∗ 10𝟑 + 10 ∗ 10𝟐 x(𝑚−1 ) – 24 ∗ 10𝟑𝑥 2 (𝑚−2 ) donde x esta en metros.
(a) Determine el trabajo hecho por el gas sobre la bala cuando esta recorre la longitud del cañón,
(b) si éste, tiene una longitud de 80 cm ¿Cuánto trabajo se realiza y como se compara este valor con el obtenido en a)?.
5. Una fuerza 𝑭⃗ = (𝟑. 𝟎𝟎𝒊̂+ 𝟒. 𝟎𝟎𝒋̂)𝑵 actúa sobre una partícula. El ángulo entre 𝑭⃗ y el vector desplazamiento 𝒔⃗ es de 𝟑𝟐. 𝟎 𝒐 , y 𝑭⃗ efectúa 96. 0 J de trabajo. Determina el vector y la magnitud del vector 𝒔⃗ , teniendo en cuenta que el ángulo que forma el vector 𝒔⃗ con el x+ , es mayor que el ángulo que forma el vector 𝑭⃗ con el x+.
6. La fuerza que actúa sobre una partícula varía como se muestra en la figura. Encuentre el trabajo invertido por la fuerza en la partícula conforme se mueve…
(a) De 𝑥 = 0.00 𝑚 a 𝑥 = 8.00 m;
(b) de 𝑥 = 0.00 𝑚 a 𝑥 = 12.00 m.
(c) Existe cierto punto A sobre el eje X tal que el trabajo realizado por esta fuerza en el intervalo [𝑥𝐴 ,12.0 m] vale cero. Encuentre el valor de 𝑥𝐴 .
7. Una bala de 60 g se dispara de un rifle que tiene un cañón de 0.40m de largo. Se considera que el origen se sitúa donde la bala empieza a moverse. La fuerza en Newton, ejercida sobre la bala por la expansión del gas es 15 ∗ 10𝟑 + 10 ∗ 10𝟐 x(𝑚−1 ) – 24 ∗ 10𝟑𝑥 2 (𝑚−2 ) donde x esta en metros.
(a) Determine el trabajo hecho por el gas sobre la bala cuando esta recorre la longitud del cañón,
(b) si éste, tiene una longitud de 80 cm ¿Cuánto trabajo se realiza y como se compara este valor con el obtenido en a)?.
Energía cinética y el teorema del trabajo y la energía
8. Un campesino engancha su tractor a un trineo cargado con leña y lo arrastra 23.0 m sobre el suelo horizontal. El peso total del trineo y la carga es de 1.98*104 N. El tractor ejerce una fuerza constante de 5.6*103 N a 𝟑𝟕. 𝟓 𝟎 sobre la horizontal. Una fuerza de fricción de 2.9*103 N se opone al movimiento del trineo.
(A) Calcule el trabajo realizado por CADA fuerza que actúa sobre el trineo
(B) el trabajo total o trabajo neto de todas las fuerzas y
(C) la velocidad que lleva en el momento que ha recorrido los 23.0 m.
9. Un vagón de 5.00 × 103 kg rueda a lo largo de una vía recta con fricción despreciable. El vagón se lleva al reposo mediante una combinación de dos resortes de espiral, como se ilustra en la figura. Ambos resorte se describen mediante la Ley de Hooke con 𝑘1 = 1.60 × 103 N/m y 𝑘2 = 3.40 × 103 N/m. Después de que el primer resorte se comprime una distancia de 30.0 cm, el segundo resorte actúa junto con el primero para aumentar la fuerza mientras se presenta una compresión adicional como se muestra en la gráfica. El vagón llega al reposo 20.0 cm después de que empieza a obrar también el segundo resorte. Encuentre la rapidez inicial del vagón.
8. Un campesino engancha su tractor a un trineo cargado con leña y lo arrastra 23.0 m sobre el suelo horizontal. El peso total del trineo y la carga es de 1.98*104 N. El tractor ejerce una fuerza constante de 5.6*103 N a 𝟑𝟕. 𝟓 𝟎 sobre la horizontal. Una fuerza de fricción de 2.9*103 N se opone al movimiento del trineo.
(A) Calcule el trabajo realizado por CADA fuerza que actúa sobre el trineo
(B) el trabajo total o trabajo neto de todas las fuerzas y
(C) la velocidad que lleva en el momento que ha recorrido los 23.0 m.
9. Un vagón de 5.00 × 103 kg rueda a lo largo de una vía recta con fricción despreciable. El vagón se lleva al reposo mediante una combinación de dos resortes de espiral, como se ilustra en la figura. Ambos resorte se describen mediante la Ley de Hooke con 𝑘1 = 1.60 × 103 N/m y 𝑘2 = 3.40 × 103 N/m. Después de que el primer resorte se comprime una distancia de 30.0 cm, el segundo resorte actúa junto con el primero para aumentar la fuerza mientras se presenta una compresión adicional como se muestra en la gráfica. El vagón llega al reposo 20.0 cm después de que empieza a obrar también el segundo resorte. Encuentre la rapidez inicial del vagón.
10. Una polea con su respectiva cuerda se usa para levantar una persona que se encuentra en un pozo estrecho y de gran
profundidad, la persona lleva un maletín que produce un rozamiento contra las paredes del pozo, lo cual generan una
fuerza de fricción constante de 400N. Masa de la persona: 78Kg; Peso del maletín: 8Kg. ¿Cuánta potencia debe
proporcionar el motor de la polea para levantar la persona a una rapidez constante de 1,00 m/s?.












0 Comentarios
Si necesitas la solución de algún Trabajo o Ejercicios enviala al correo saemaster10@gmail.com con la fecha que la necesitas y te responderemos el costo de la realización